Subtask 1: Có thể được giải quyết theo nhiều cách. Chúng tôi sẽ mô tả giải pháp sử dụng hashing, phương pháp này sẽ hữu ích cho subtask cuối cùng. Hãy root cây tại một nút $R$. Chúng ta quan tâm đến tất cả các đoạn palindromic có một đầu nằm tại nút $R$. Với mỗi nút $X$, chúng ta sẽ tính hai giá trị:

Ở đây, $x_0, x_1, \ldots, x_{k-1}$ là một mảng các màu trên đường đi từ $R$ đến $X$ (với $\text{color}(R) = x_0$, $\text{color}(X) = x_{k-1}$) và $B$ là giá trị của cơ sở hash. Hai giá trị này có thể được xác định bằng một lần duyệt DFS duy nhất trên cây.

Đường đi từ $R$ đến $X$ là một đoạn palindromic nếu $down_X = up_X$. Nếu chúng ta root cây tại mỗi nút và áp dụng quy trình này, chúng ta sẽ bao quát được tất cả các trường hợp. Độ phức tạp của thuật toán này là $O(N^2)$.

Subtask 2: Đây là bài toán kinh điển, rất quen thuộc về việc tìm đoạn con palindromic dài nhất, có thể được giải bằng thuật toán Manacher. https://en.wikipedia.org/wiki/Longest_palindromic_substring

Giải pháp cho subtask thứ ba khá giống với giải pháp của subtask thứ hai. Điểm khác biệt duy nhất là chúng ta phải áp dụng thuật toán Manacher trên đường đi giữa mọi cặp lá.

Chúng ta sẽ bắt đầu giải pháp cho toàn bộ bài toán với quan sát sau: Nếu tồn tại một đoạn palindromic có độ dài $K>2$, thì chắc chắn tồn tại một đoạn palindromic có độ dài $K-2$. Do đó, chúng ta có thể sử dụng tìm kiếm nhị phân trên các độ dài

chẵn và lẻ để tìm đoạn palindromic dài nhất.

Nhưng làm thế nào để kiểm tra xem có tồn tại một đoạn palindromic với độ dài cố định trong một cây bất kỳ? Để trả lời câu hỏi này, trước tiên chúng ta sẽ giải một phiên bản đơn giản hơn của bài toán – kiểm tra xem có đoạn palindromic với độ dài

cố định chứa gốc của cây, nút $R$, hay không.

Trong một cây có gốc, đường đi giữa hai nút $A$ và $B$ bao gồm hai nhánh cây, trong đó độ dài đường đi trên một nhánh lớn hơn hoặc bằng độ dài trên nhánh còn lại. Chúng ta sẽ chia đường đi giữa $A$ và $B$ thành ba phần: đường đi từ $A$ đến $C$,

đường đi từ $C$ đến gốc $R$, và đường đi từ $R$ đến $B$, trong đó $C$ được chọn sao cho độ dài $A-C$ và $R-B$ bằng nhau. Lưu ý rằng $C$ được xác định duy nhất bởi nút $A$, vì chúng ta chỉ quan tâm đến các palindrome có độ dài cố định.

Để kiểm tra xem đường đi từ $A$ đến $B$ có phải là một đoạn palindromic hay không, chúng ta chỉ cần kiểm tra các điều kiện sau:

1. Đường đi từ $R$ đến $C$ là một palindrome (được biểu diễn bằng màu đỏ).
2. Các màu từ $C$ đến $A$ giống với các màu từ $R$ đến $B$ (được biểu diễn bằng màu xanh).

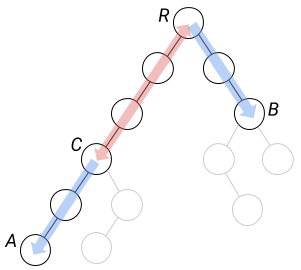
Với mỗi nút của cây, chúng ta sẽ tính trước các giá trị $\text{down}_X$ và $\text{up}_X$ theo cách đã được mô tả trong lời giải của subtask đầu tiên. Việc kiểm tra đầu tiên được thực hiện đơn giản bằng cách so sánh $\text{down}_C$ và $\text{up}_C$. Việc kiểm tra thứ hai có thể được thực hiện bằng cách so sánh các giá trị sau:

trong đó $\text{par}(C)$ là cha của nút $C$ và $\text{dep}(X)$ là độ sâu của nút $X$.

Gọi $S_B$ là tập hợp các hash, trong đó chúng ta sẽ chèn các giá trị $\text{down}_B$ của tất cả các nút $B$ trong cây. Với một nút $A$ cố định, chúng ta có thể kiểm tra điều kiện (1) và kiểm tra điều kiện (3) bằng cách tìm giá trị tương ứng trong $S_B$. Giả định rằng độ phức tạp của tất cả các thao tác với $S_B$ là hằng số nếu sử dụng một bảng hash (ví dụ: \texttt{std::unordered_set} trong C++). Do đó, độ phức tạp của toàn bộ kiểm tra là $O(N)$.

Note:
Trong quá trình triển khai, cần đảm bảo rằng tổ tiên chung thấp nhất (LCA) của các nút trong $S_B$ và $A$ là nút gốc $R$.

Bây giờ khi biết liệu có tồn tại một đoạn palindromic với độ dài nhất định đi qua gốc $R$ hay không, chúng ta có thể sử dụng phân rã trọng tâm (centroid decomposition). Kiểm tra này cho mỗi cây con được phân rã với trọng tâm là gốc sẽ bao quát được tất cả các trường hợp. Kết hợp phân rã trọng tâm và tìm kiếm nhị phân, chúng ta có một thuật toán với độ phức tạp $O(N \log^2 N)$.